Hello! Today I want to talk about maximization, and I will explain why.
As part of my research, I have been working with networks and with a relatively simple maximization problem, in order to study how information flows across agents, namely, how can high-level information agents affect low-level information agents, as well as if there is any externality of heterogenous communities. This could be relevant because of policy implications, such as affordable rent ideas: allowing (or forcing) the existence of cheaper living units in rich neighborhoods. The main driver would be network effects.
Now, I want to talk about the maximization problem I faced, which in my opinion is usually overlooked in the textbooks, and that is not trivial how to correctly formulate. Basically I had a problem like the one described in the following picture. Suppose you know $x_2$, but neither $x_1$ or $x_3$, and you need to maximize your choice of investment with that information. How do you do this? Suppose $p_1$ represents the probability that $x_1 = F$, and that $p_3$ represents the probability that $x_3 = F$. Furthermore, suppose the problem is symmetric, to make it simple.
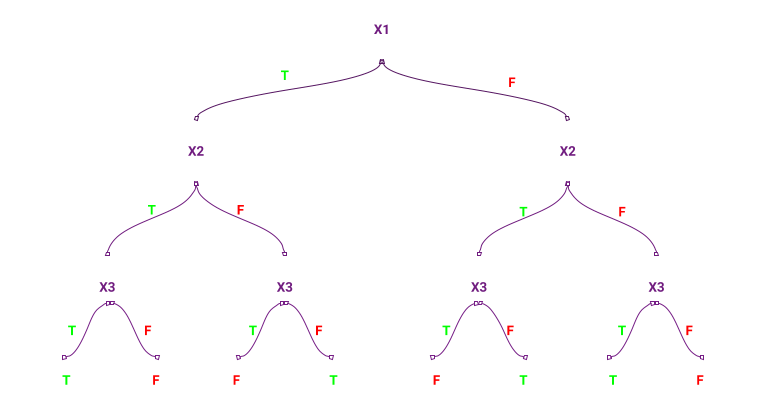
One way to do this would be to solve
$$ \max_{decision1} p_1 ( p_3 * f(decision_1 |x_1 = F) + (1-p_3) * f(decision_1|x_1 = F) ) + (1-p_1) ( p_3 * f(decision_1 |x_1 = T) + (1-p_3)* f(decision_1 |x_1 = T)),$$
but another way to solve it would be to do instead:
$$ \max_{decision1} p_3 ( p_1 * f(decision_1 |x_3 = F) + (1-p_1) * f(decision_1|x_3 = F) ) + (1-p_3) ( p_1 * f(decision_1 |x_3 = T) + (1-p_1)* f(decision_1 |x_3 = T)),$$
Perhaps you find the solution trivial, but it’s not. Think about it this way: which variable should you condition on? If you frame it like that, it seems obvious that one should condition on $x_1$, and that turns out to be the right answer. I write about this because this was a problem that got me stuck for a while. It is the kind of things that one learns at school without really asking or wondering why, but that faced with the problem, it becomes clear.
I hope you find this useful. I finish by including a picture of a recent hike, this time in Mineral del Chico.


